The Great Elephant Race

2025-08-31

Background

While at work last week, my coworker gave me an interesting riddle. After working through it myself and giving it to some friends, I decided to make a little write up on the riddle and its solutions.

The Riddle

There are 900 elephants in a race. Bob and Charlie know which elephants are in 1st and 2nd place.

You are allowed to ask Bob a question about the race that he will respond to with a number from 1 to $n$. After that Charlie will give you the number of either the 1st or 2nd place elephant.

You have to use Bob's answer to determine whether Charlie's number is the 1st or 2nd place elephant.

What is the lowest upper bound of $n$ Bob can give you so that you can determine if the elephant Charlie gave you finished in 1st or 2nd?

Clarifications

Can you ask Bob which elephant got first place?

Yes, if you ask Bob who got first place, you can use his answer to determine whether the elephant Charlie gives placed 1st or 2nd. However the upper bound for $n$ in this case is 900 (there are better answers).

Can Bob answer with fractions or decimals?

No, he must either answer with whole numbers or have the ability to map his possible answers to whole numbers.

Can you ask Bob multiple questions?

You can make the question you ask Bob as long as you want. However, Bob is only allowed to answer with a single number. You are allowed to make each digit depend on a sub-question, but then the lowest upper bound would be the range of possibilities that Bob would answer with.

For example, you could ask Bob 2 yes or no questions and have him answer with a 2 digit number (1 digit per question) where 1 means yes and 2 means no. Since there would be 4 possible answers Bob could give (11,12,21,22), the upper bound for $n$ would be 4.

This Sounds Like a Math Problem?

What problem isn't a math problem! Here's a version of the riddle formatted as a math question:

• Let $A$ = The set of answers Bob can give
• Let $E$ = The set of unique elephants in the race
• Let $\mathcal{F} = \{f : E \times E \times A \to \{0,1\}\}$ be the set of questions you can ask Bob where:
  • $f(\text{🐘}_a, \text{🐘}_b, \text{ans}) = 1$ if elephants $\text{🐘}_a$ and $\text{🐘}_b$ can be distinguished using Bob's answer $\text{ans}$
  • $f(\text{🐘}_a, \text{🐘}_b, \text{ans}) = 0$ otherwise

Find the minimum possible $|A|$ such that:

$$\begin{align*} &\forall \text{🐘}_a, \text{🐘}_b \in E, \\ &\exists \text{ans} \in A, \\ &\exists f \in \mathcal{F} : \\ &(\text{🐘}_a = \text{🐘}_b) \implies (f(\text{🐘}_a, \text{🐘}_b, \text{ans}) = 1) \end{align*}$$

Can Bob tell the future?

A peculiar individual asked me this question to which I answered yes out of curiosity. He then answered: "I would ask Bob to say 1 if Charlie is going to say the 1st place elephant, and 2 if Charlie says the 2nd place elephant". I have not seen a solution with a lower bound than this.

The Intuitive Solution

A non-optimal but still efficient way of solving this problem is as follows:

1. Have Bob tell you a position of the first digit in the 1st place elephant that is different in the 2nd place elephant.
   • He will say 1 if it's the ones digit, 2 if it's the tens digit, and 3 if it's the hundreds digit.
2. Have Bob tell you what the value of that digit is for the 1st place elephant.
   • He will answer this as a number from 0-9.
3. Have Bob combine the 2 numbers as his answer

Since there are 30 possible answers Bob can give (3 max digits $\times$ 10 possible values), the lowest upper bound that Bob can give you is $n = 30$.

Example of the Solution

• Let the 1st place elephant be $\text{🐘}_{45}$ and the 2nd place elephant be $\text{🐘}_{149}$
• Bob will answer "15" since the ones digit is is "5" in the 1st place elephant and "9" in the 2nd place elephant
• There are 2 numbers that Charlie can give you:
  • If Charlie gives you the 1st place elephant ($\text{🐘}_{45}$), you can see that the ones place digit is "5". Since you know the 1st place elephant has this characteristic and the 2nd place elephant doesn't, this must be the 1st place elephant.
  • If Charlie gives you the 2nd place elephant ($\text{🐘}_{149}$), you can see that the ones place digit is "9". Since you know the 1st place has a "5" in the ones place, this must be the 2nd place elephant.

Optimizations

The intuitive solution assumes a base 10 number system. Surprisingly, different number systems like Base 12 and Base 7 will give different answers. Below is a more general approach that accounts for different bases:

1. Let $B$ be the base of the chosen number system (decimal, binary, etc.)
2. Determine the maximum number of digits needed to represent 900
   • We'll refer to this as $D$
   • $D = \lceil \log_B(900) \rceil$
3. Have Bob return position of digit along with value
   • Bob will answer in format $(d, v)$ where $d \in [1, D]$ and $v \in [0, B-1]$
     • $d$ represents the digit position (1st, 2nd, 3rd, etc.)
     • $v$ represents the digit value in base $B$

In this solution, the minimum upper bound of answers will be $n = D \times B$. However, since we know that $D = \lceil \log_B(900) \rceil$, we can simplify the upper bound to $n = \lceil \log_B(900) \rceil \times B$. Below are some example bases and their respective results:

$B$ (Base)	$\lceil \log_B(900) \rceil$ (Digits Needed)	$D \times B$ (Min Upper Bound)
2	10	20
3	7	21
5	4	20
7	4	28
9	4	36
10	3	30
12	3	36
30	2	60

What's Going on Here?

Why does changing the base of the number system change the minimum upper bound so much? To answer this, let's dive deeper into what's happening in our solution. When we choose a base for our strategy, we're implicitly creating $D \times B$ different groupings of elephants. Each group is defined by fixing a value of a specific digit to a constant value.

Here are the groupings for $B=10$ with padded zeros to more clearly show the pattern:

Group	Bob's Label	Elephants in Group
$G_{1}$	(1,0)	$\text{🐘}_{000}$1, $\text{🐘}_{010}$, $\text{🐘}_{020}$, ..., $\text{🐘}_{970}$, $\text{🐘}_{980}$, $\text{🐘}_{990}$
$G_{2}$	(1,1)	$\text{🐘}_{001}$, $\text{🐘}_{011}$, $\text{🐘}_{021}$, ..., $\text{🐘}_{971}$, $\text{🐘}_{981}$, $\text{🐘}_{991}$
$G_{3}$	(1,2)	$\text{🐘}_{002}$, $\text{🐘}_{012}$, $\text{🐘}_{022}$, ..., $\text{🐘}_{972}$, $\text{🐘}_{982}$, $\text{🐘}_{992}$
...	...	...
$G_{28}$	(3,7)	$\text{🐘}_{700}$, $\text{🐘}_{701}$, $\text{🐘}_{702}$, ..., $\text{🐘}_{797}$, $\text{🐘}_{798}$, $\text{🐘}_{799}$
$G_{29}$	(3,8)	$\text{🐘}_{800}$, $\text{🐘}_{801}$, $\text{🐘}_{802}$, ..., $\text{🐘}_{897}$, $\text{🐘}_{898}$, $\text{🐘}_{899}$
$G_{30}$	(3,9)	$\text{🐘}_{900}$, $\text{🐘}_{901}$, $\text{🐘}_{902}$, ..., $\text{🐘}_{997}$, $\text{🐘}_{998}$, $\text{🐘}_{999}$1

Since there are 2 digits unconstrained in each group, there are $10^2=100$ elements per group¹. This means the total number of elephants including duplicates is $30 \times 100 = 3000$, meaning each elephant appears in exactly 3 groups ¹.

Using the Groups

Now let's explore why this way of grouping elephants helps Bob answer our question. When we ask Bob to tell us which digit is different and the value it should be, we're essentially asking Bob to tell us which of the above groups contains the 1st place elephant but not the 2nd place elephant. Once Bob gives us a group, we just check if the elephant Charlie gives us is in that group. If it's in the group, Charlie gave us the 1st place elephant. Otherwise we know it's the 2nd place elephant.

We know that there is guaranteed to be a group that contains 1st place but not 2nd place because of two reasons:

1. The 1st and 2nd place elephants are represented by two different numbers
2. Every pair of 2 distinct numbers must have at least 1 different digit for all number systems

The Advanced Answer

With the previous strategy, we discovered that we are actually turning the 900 elephants into 30 groups (for $B=10$) such that for distinct values $\text{🐘}_a$ and $\text{🐘}_b$ (1st and 2nd place elephants), there is guaranteed to be a group that contains $\text{🐘}_a$ but not $\text{🐘}_b$.

Now we wish to determine the minimum number of groups we need to be able to distinguish the 1st from 2nd elephant given 900 distinct elephants.

Grouping by Hand

Let's start by hand choosing groups for smaller numbers of elephants:

Num Elephants = 3	Num Elephants = 4	Num Elephants = 5
$G_1 = \{\text{🐘}_1, \text{🐘}_2\}$	$G_1 = \{\text{🐘}_2, \text{🐘}_3\}$	$G_1 = \{\text{🐘}_1, \text{🐘}_2, \text{🐘}_3\}$
$G_2 = \{\text{🐘}_1, \text{🐘}_3\}$	$G_2 = \{\text{🐘}_1, \text{🐘}_4\}$	$G_2 = \{\text{🐘}_1, \text{🐘}_4, \text{🐘}_5\}$
$G_3 = \{\text{🐘}_2, \text{🐘}_3\}$	$G_3 = \{\text{🐘}_2, \text{🐘}_4\}$	$G_3 = \{\text{🐘}_2, \text{🐘}_4\}$
	$G_4 = \{\text{🐘}_1, \text{🐘}_3\}$	$G_4 = \{\text{🐘}_3, \text{🐘}_5\}$

These groupings work because all elephants appear in at least 2 groups which have no shared items besides the elephant in question. This means then for all possible 1st and 2nd place pairs that Charlie can give, Bob can give the number of the group containing only the 1st place elephant.

A Better Representation

Now let's try to generalize this to larger groups of elephants. Instead of explicitly showing the groups, let's assume $n$ groups and give each elephant an $n$ length encoding that says what groups they are a part of. For position $i$ of the encoding, let 1 signal that the elephant is part of group $i$ and 0 that the elephant is not in group $i$.

Using the Representation

To determine if any 1st and 2nd place elephant pair Charlie can give is valid, we can now just compare each elephant's encoding to see if there is a position where 1st place has a 1 and 2nd place has a zero.

Below is an example of how you could use the above encoding to determine:

• 1st Place = $\text{🐘}_3$ and 2nd Place = $\text{🐘}_5$
• Encodings:
  • $\text{🐘}_3 = 1001$
  • $\text{🐘}_5 = 0101$
• Since Position 1 for 1st place elephant is 1 while 0 for 2nd place elephant, we know Group 1 contains 1st place elephant and not 2nd place elephant. Therefore Bob will answer Group 1.
• There are 2 numbers that Charlie can give you:
  • If Charlie gives you the 1st place elephant ($\text{🐘}_3$), we see from $\text{🐘}_3$'s encoding (1001) that it is in Group 1 and therefore must be the 1st place elephant.
  • If Charlie gives you the 2nd place elephant ($\text{🐘}_5$), we see from $\text{🐘}_5$'s encoding (0101) that it isn't in Group 1 and therefore must be the 2nd place elephant.

The Underlying Pattern

If you look closely you'll also notice that each elephant encoding has exactly 2 1s in its encoding of length 4. An interesting property of this representation is that as long as every elephant is in exactly $k$ groups (when a 1 appears $k$ times in the elephants encoding), then for any 2 elephants $\text{🐘}_{a}$ and $\text{🐘}_{b}$, there will be a position in the encoding such that elephant $\text{🐘}_{a}$ will have value 1 while elephant $\text{🐘}_{b}$ has value 0. In the original solution, each elephant appeared in exactly 3 different groups out of the 30 total showing it also follows this pattern.

What are the rules for picking the number of groups ($n$) and number of 1s ($k$) allowed for each encoding? With $n$ groups and a fixed $k$, we can derive the number of unique encodings with $\binom{n}{k}$. So for our example above when $n=4$ and $k=2$, we can uniquely represent a max of $\binom{4}{2}=6$ elephants.

We now need to find the optimal $k$ such that we can minimize $n$ for 900 elephants. To do this, we need to find the minimum $n$ such that $\exists k: \binom{n}{k} \geq 900$. Before we try to solve that directly², let's try and simplify the problem a little more.

Optimizing the Pattern

You may notice when you plug in $\binom{n}{k}$ with different $n$ and $k$ values, it tends to be maximal for a given $n$ when we choose a $k$ that is about $n/2$. This can be formalized with the below theorem:

Sperner's Theorem: The largest possible family of non-overlapping subsets for an $n$ sized set can be calculated as:

$|S| \leq \binom{n}{\left\lfloor n/2 \right\rfloor}$

If and only if each subset has size $k = \left\lfloor \frac{n}{2} \right\rfloor$ or $k = \left\lceil \frac{n}{2} \right\rceil$

We can now use this theorem to more simply represent the problem. Let's start by testing values $n$ with the equation $900 \leq \binom{n}{\left\lfloor n/2 \right\rfloor}$ on different values until we find the minimum number of groups that work.

If we try with $n=11$, we get $\binom{11}{\left\lfloor 11/2 \right\rfloor} = \binom{11}{5} = 462$. This shows us we need more than 11 groups as $462 < 900$.

If we try with $n=12$, we get $\binom{12}{\left\lfloor 12/2 \right\rfloor} = \binom{12}{6} = 924$. As $924 > 900$ we know this is a valid number of groupings. Additionally, since we know $n=11$ doesn't work and we need to use whole numbers for numbers of groups, the minimum upper bound Bob can give is $n=12$ ³.

We can generalize this to different sized elephant races by using a binary search from 2 to the size of the race to find the minimum number of groups using the above equation. I created a handy little visualization tool to help create visualizations for generating the optimal groups below:

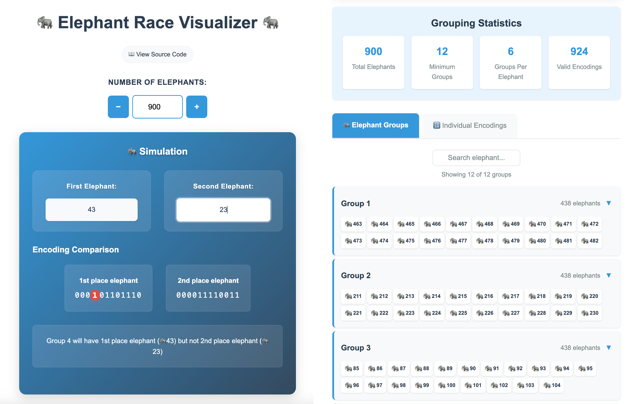
Conclusion

In this post, we first determined a way to distinguish any 2 elephants of a 900 elephant race from a set of 30 possible answers based on the digits of the elephants' numbers. We then discovered we can lower the set of possible answers to 20 by using a different number system such as binary instead of decimal. After this we dug deeper into why this trick worked and used the intuition to calculate the smallest possible set of answers³ which turned out to be 12.

The next time you're at an elephant race and have an annoying friend named Charlie who loves giving cryptic answers, make sure you use this strategy when you talk to Bob!

Footnotes

1. We're including $\text{🐘}_{000}$ and any elephant above 900 in these calculations despite them not being in the race. This is because you can use this strategy for races of up to 1000 elephants. ↩︎ ↩︎ ↩︎ ↩︎

2. You can plug this in to Desmos to solve ↩︎

3. This is the minimum bound with this method, there may or may not be an even lower bound ↩︎ ↩︎